728x90
반응형
[백준] 6549 히스토그램에서 가장 큰 직사각형 풀이
자료 구조, 세그먼트 트리, 분할 정복, 스택
문제 출처:
https://www.acmicpc.net/problem/6549
6549번: 히스토그램에서 가장 큰 직사각형
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤
www.acmicpc.net
문제 요약
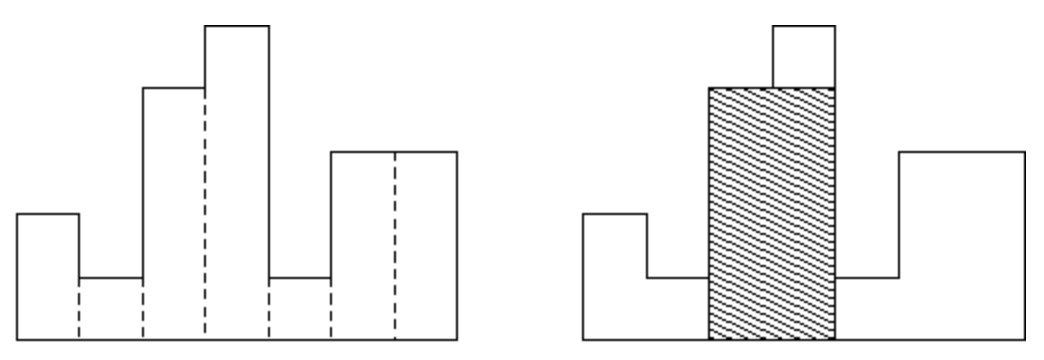
- 배열의 형태로 직사각형의 높이를 입력받는다(너비는 1로 동일하다). 이 때 직사각형의 최대 넓이를 찾으면 된다.
풀이 정리
1. 알고리즘 수업 시간에 주식 변동 값이 배열로 주어질 때 언제 사고 파는 것이 적기인가를 구하는 문제와 비슷했기 때문에, '분할 정복'으로 풀 수 있었다. 교수님 과제 채점 기준으로, 이 방법은 만점을 받지 못하고 8~9점 대에서 머물렀다. -> 분할정복 시간복잡도 O(NlogN)
2. 다른 방법을 찾아보니 '스택' 자료구조를 활용하는 방법이 있었다. 이 방법으로 10점을 받을 수 있었다. -> 스택 시간복잡도 O(N)
java 코드
import java.io.*;
import java.util.Stack;
public class histogramToRect{
private int[] length;
public histogramToRect(int[] l){
int i=0, n = l.length;
this.length = new int[n];
for(i=0;i<n;i++)
this.length[i] = l[i];
}
public void printSticks(){
int i=0, n=length.length;
System.out.println("n = " + n);
System.out.print("lengths: ");
for(i=0;i<n;i++)
System.out.print(length[i] + " ");
System.out.println();
}
public int maxArea(){
int n=length.length;
return getArea(0, n-1); //Divide and Conquer
return getArea(); //Using Stack
}
//O(n) using stack
public int getArea(){
Stack<Integer> stack = new Stack<>();
int maxArea = 0;
int i = 0;
while(i<length.length){
if(stack.isEmpty() || length[i] >= length[stack.peek()]){
stack.push(i);
i++;
}
else{
int top = stack.pop();
int width = stack.isEmpty() ? i : i-stack.peek()-1;
maxArea = Math.max(maxArea, length[top]*width);
}
}
while(!stack.isEmpty()){
int top = stack.pop();
int width = stack.isEmpty() ? i : i-stack.peek()-1;
maxArea = Math.max(maxArea, length[top]*width);
}
return maxArea;
}
// O(nlogn) divide and conquer
public int getArea(int left, int right) {
if(left == right) return length[left];
int mid = (left + right) / 2;
int maxArea = Math.max(getArea(left, mid), getArea(mid + 1, right));
int low = mid, high = mid + 1;
int height = Math.min(length[low], length[high]);
maxArea = Math.max(maxArea, height * 2);
while(left < low || high < right) {
if(high < right && (low == left || length[low - 1] < length[high + 1])) {
high++;
height = Math.min(height, length[high]);
}
else {
low--;
height = Math.min(height, length[low]);
}
maxArea = Math.max(maxArea, height * (high - low + 1));
}
return maxArea;
}
// O(nlogn) divide and conquer
public int getArea(int low, int high){
if(low==high){
return length[low];
}
int mid = (low+high)/2;
int leftArea = getArea(low, mid);
int rightArea = getArea(mid+1, high);
int maxArea = Math.max(leftArea, rightArea);
maxArea = Math.max(maxArea, getMidArea(low, high, mid));
return maxArea;
}
public int getMidArea(int low, int high, int mid){
int toLeft = mid;
int toRight = mid;
int height = length[mid];
int maxArea = height;
while(low < toLeft && toRight < high){
if(length[toLeft-1] < length[toRight+1]){
toRight++;
height = Math.min(height, length[toRight]);
}
else{
toLeft--;
height = Math.min(height, length[toLeft]);
}
maxArea = Math.max(maxArea, height * (toRight-toLeft+1));
}
while(toRight < high){
toRight++;
height = Math.min(height, length[toRight]);
maxArea = Math.max(maxArea, height * (toRight-toLeft+1));
}
while(low < toLeft){
toLeft--;
height = Math.min(height, length[toLeft]);
maxArea = Math.max(maxArea, height * (toRight-toLeft+1));
}
return maxArea;
}
}
728x90
반응형
'알고리즘 > 백준' 카테고리의 다른 글
| [cpp 알고리즘] 백준 1780 종이의 개수 (0) | 2023.11.09 |
|---|---|
| [cpp 알고리즘] 백준 1992 쿼드트리 (2) | 2023.11.08 |
| [알고리즘 cpp] 백준 23246 Sport Climbing Combined (0) | 2023.10.11 |
| [cpp 알고리즘] 백준 25943 양팔저울 (1) | 2023.09.27 |
| [C++ 알고리즘] 백준 14444 가장 긴 팰린드롬 부분 문자열 (2) | 2023.05.23 |


