네트워크 플로우(Network Flow) 알고리즘이란?
- 그래프에서 두 정점 사이에 얼마나 많은 유량(flow)을 보낼 수 있는지 계산하는 알고리즘
- 그래프 내 source 정점에서 유량을 발생시켜 간선을 통해 sink 정점에 도달시키는 것이 목표
= 최대 유량(Maximum Flow) 알고리즘
기본 용어 정리
용량 (Capcity, c(u,v)) : 정점 u에서 v로 가는 간선에 흐를 수 있는 최대 유량(가중치)
유량 (Flow, f(u,v)) : 정점 u에서 v로의 간선에 실제로 흐르는 유량
잔여 용량 (Residual Capacity: r(u,v)) : c(u,v) - f(u,v)
소스 (Source) : 유량이 시작되는 정점
싱크 (Sink) : 모든 유량이 도착하는 정점
증가 경로 (Augmenting Path) : 유량이 흐를 수 있는 source에서 sink까지 가는 경로
유량 상쇄 : 모든 경로에 기존에 존재하는 간선들과 반대되는 방향의 간선을 추가한 뒤, 각 간선으로 유량을 흘려보냈을 때, 반대 방향의 간선으로도 음의 유량을 흘려보냄으로써 유량을 상쇄시키는 것. 음의 유량을 기록함으로써, 잔여 용량을 남겨 추가적인 경로를 탐색할 수 있도록 하기 위한 작업. 두 정점이 서로에게 유량을 보내주는 것은 의미가 없기 때문에 성립 가능.
속성
1. 특정 경로를 따라 유량을 보낼 때, 그 경로에 포함된 간선 중 가장 용량이 작은 간선에 의해 유량이 결정된다.

- Source-> A의 용량은 7, A->B의 용량은 5, B->Sink의 용량은 9라고 할 때,
가장 용량이 작은 간선인 A->B을 기준으로 유량이 결정된다. 따라서 유량 flow의 값은 5이다.
Q) 만약 source에서 7의 유량을 내보낸다면?

- A -> B 간선 사이에서 Capcity보다 큰 Flow 값이 들어와서, 다음으로 넘어가지 않는다.
- 따라서 source에서 sink까지 막힘없이 흐를 수 있는 최적의 유량은 5이다.
2. 용량 제한 속성: 흐르는 양이 항상 그 간선의 용량을 넘을 수 없다.
f(u,v) <= c(u,v) : 정점 u에서 v로 흐르는 flow의 양은 capcity의 양보다 작거나 같다.
3. 유량의 대칭성
f(u,v) = -f(v,u) : 정점 u에서 v로 흐르는 flow의 값은, 정점 v에서 u로 흐르는 값과 절대값은 같고 부호는 반대이다.
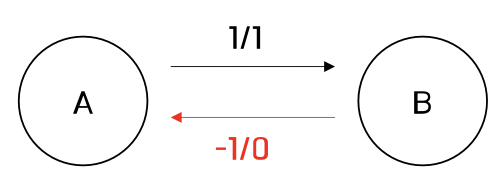
4. 유량 보존의 법칙: source와 sink를 제외한 모든 각 정점에 대해서 들어오는 유량과 나가는 유량의 양은 같다.
유량의 대칭성에 의해, ∑f(u,v) = 0
- 아래의 그림은 유량 보존의 법칙이 지켜지지 않은 경우이다.
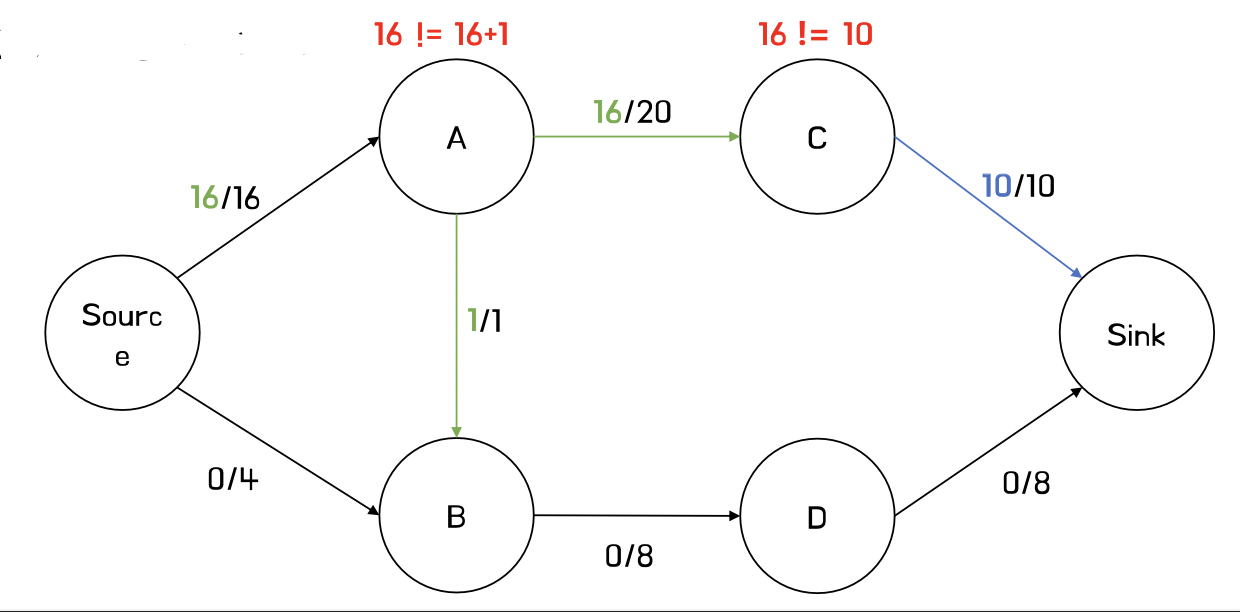
- 연두색 간선을 따라 가보면, Source -> A의 유량 값은 16인데, A에서 흘러 나가는 유량은 A -> C의 값인 16과, A -> B의 값인 1이 더해져서 17로 같지 않다.
- 정점 C를 기준으로 파란색 간선을 보면, C로 유입되는 유량의 값은 A -> C 16인데, C에서 나가는 유량은 C -> Sink 10이므로 같지 않아 지켜지지 않은 경우이다.
포드-풀커슨 (Ford-Fulkerson) 방법
: 잔여 네트워크에서 증가 경로가 더 이상 존재하지 않을 때까지 유량을 흘려 보내는 방식
- source는 1번 정점, sink는 7번 정점이라고 가정했을 때, 최대 유량의 값을 찾아보자!!!
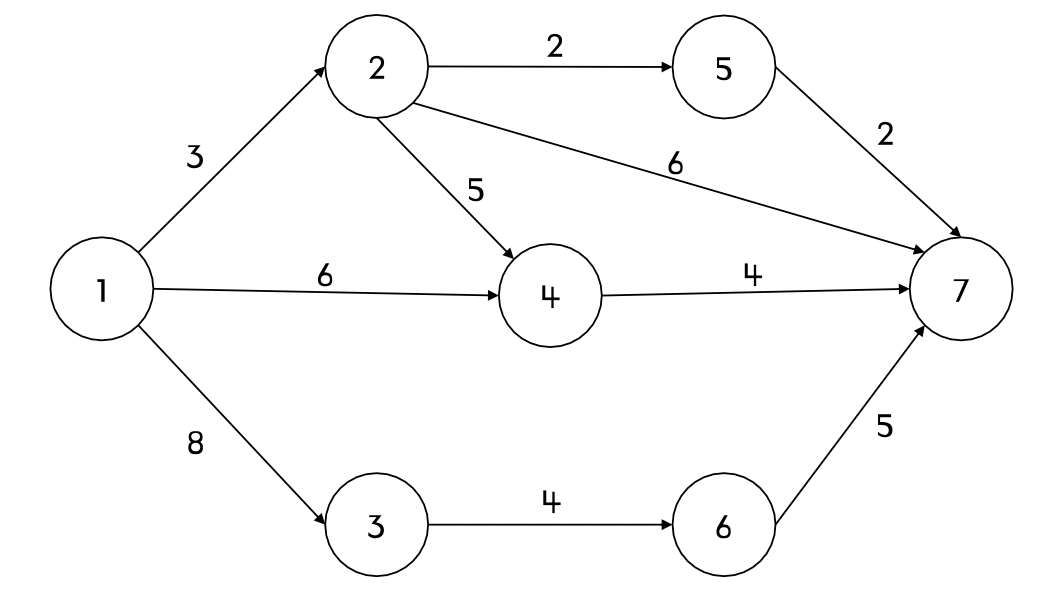
case1) 증가경로가 1 -> 2 -> 4 -> 7인 경우
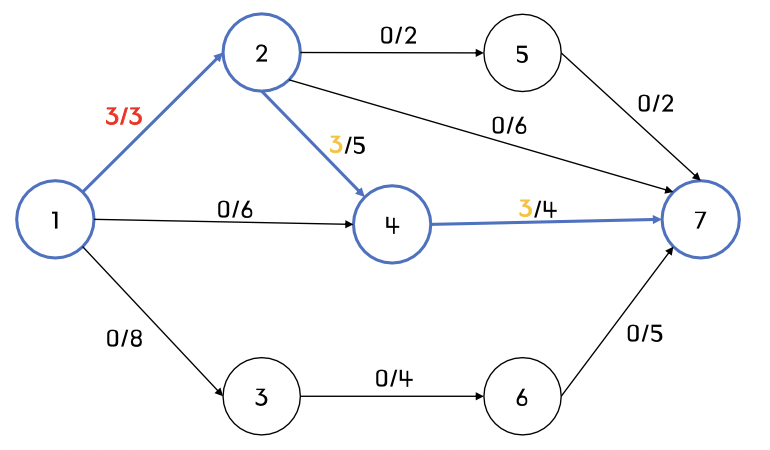
- 최대 3의 유량이 흐를 수 있다.
- 간선 1 -> 2의 유량(3)이 용량(3)에 도달했으므로 더 이상 간선 1 -> 2를 포함할 수 없다.
step2) 앞의 경우에 이어서, 증가경로가 1 -> 3 -> 6 -> 7인 경우
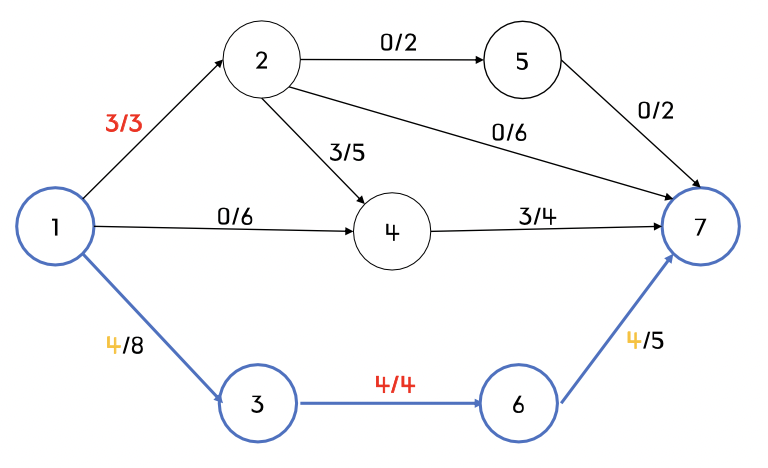
- 최대 4의 유량이 흐를 수 있다.
- 간선 3 -> 6의 유량(4)이 용량(4)에 도달했으므로,더 이상 간선 3->6을 포함할 수 없다.
step3) 앞의 경우에 이어서, 증가경로가 1 -> 4 -> 7인 경우
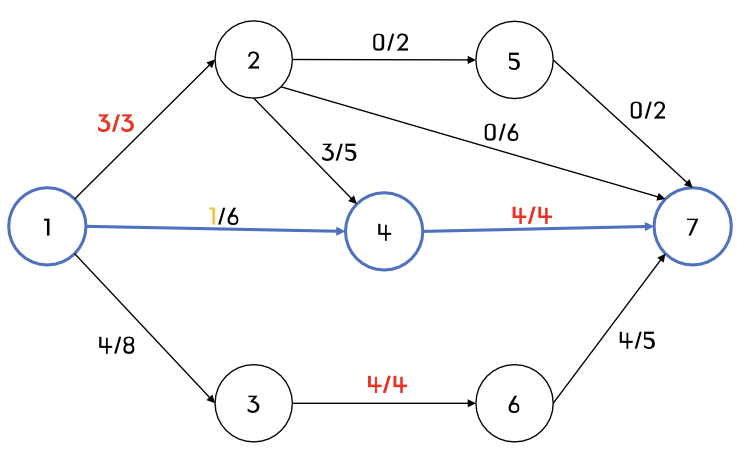
- 4 -> 7 구간의 용량은 4인데 이전까지 3의 유량이 흘렀으므로, 최대 1의 유량이 흐를 수 있다.
- 더 이상 간선 4 -> 7을 사용할 수 없다.
step4) 이렇게 까지 구하면, 현재까지의 유량은 8이다.
그러나 최대 유량의 값은 11이다. 음의 유량을 이용해 계산해보자(유량의 대칭성)
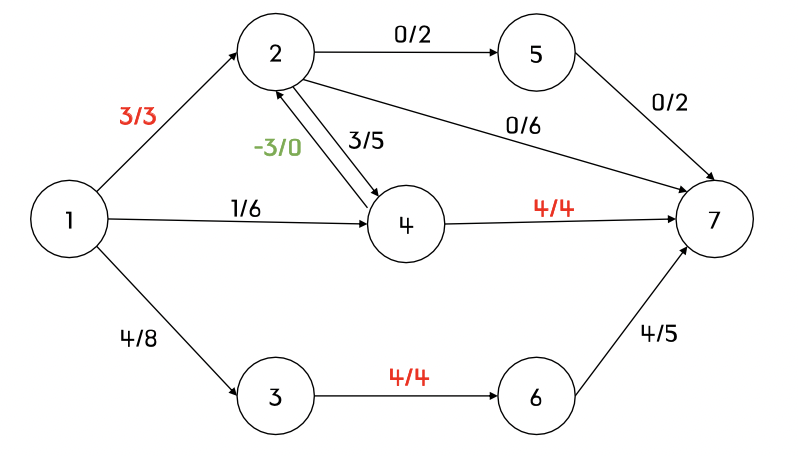
- 유량의 대칭성에 의해 f(v,u) = -f(u,v)
r(4,2) = c(4,2) - f(4,2) = 0 - (-3) = 3
step5) 증가경로가 1 -> 4 -> 2 -> 5 -> 7 인 경우
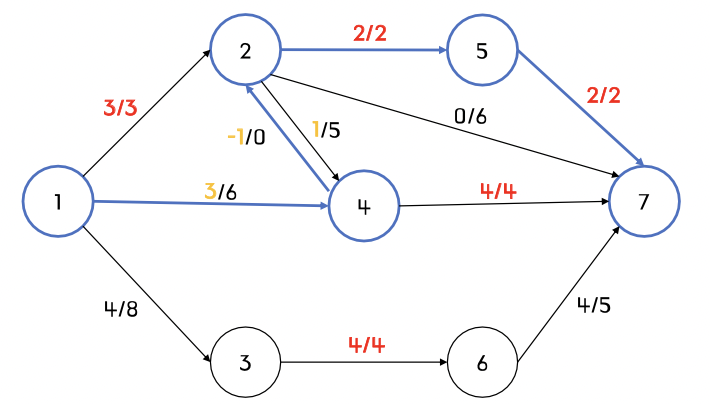
- 2 -> 5, 5 -> 7 구간의 잔여용량이 2이기 때문에, 최대 2의 유량이 흐를 수 있음
- 더 이상 간선 2 -> 5, 5 -> 7 포함 불가.
- 1 -> 4 -> 2 -> 5 -> 7 구간에서,
역방향 간선인(ex. 4 -> 2구간)는 (+) 유량으로 흐르고,
순방향 간선(ex. 1 -> 4, 2 -> 5, 5 -> 7 구간)은 (-) 유량이 흐름.
- 이전단계(8) + 현재단계(2) -> 최대 10의 유량이 흐를 수 있음.
step 6) 증가 경로가 1 -> 4- > 2 -> 7 인 경우
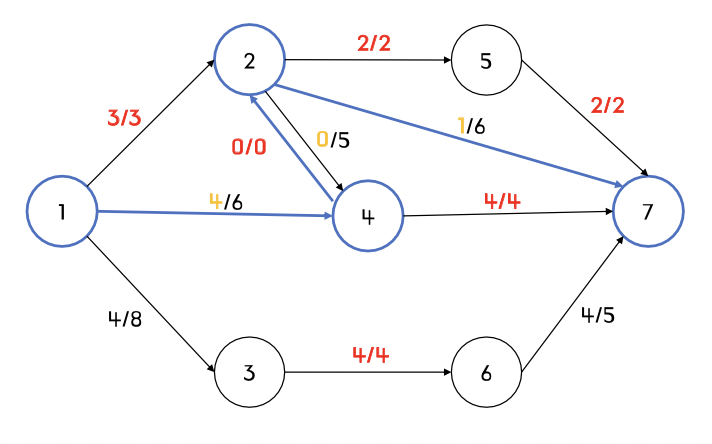
- 4 -> 2구간의 잔여 용량이 1이기 때문에, 최대 1의 유량이 흐를 수 있음
- 더 이상 가능한 증가 경로가 없음
- 이전단계(10) + 현재단계(1) -> 따라서, 최대유량의 값은 11
포드-풀커슨(Ford-Fulkerson)의 방법은 이와 같은 형식으로 이루어지며, 잔여 네트워크에서 증가 경로가 더 이상 존재하지 않을 때까지 유량을 흘려 보내는 방식이다.
진행과정
1. 네트워크에 존재하는 모든 간선(역방향 포함)의 유량을 0으로 초기화
2. source 에서 sink 로 갈 수 있는 잔여 용량이 남은 경로를 DFS 탐색
3. 해당 경로에 존재하는 간선들의 잔여 용량 중 가장 작은 값을 유량으로 흘려보냄
4. 해당 유량에 음수 값을 취해, 역방향 간선에도 흘려보냄 (-> 유량 상쇄를 위함)
5. 더 이상 잔여 용량이 남은 경로가 존재하지 않을 때까지 반복
'알고리즘' 카테고리의 다른 글
| 네트워크 플로우(Network Flow) 알고리즘, 에드몬드-카프 (Edmonds-Karp) C++ (0) | 2023.05.22 |
|---|---|
| Hash (해시) (0) | 2022.03.14 |
| Binary Search (이진 탐색) (0) | 2022.03.13 |
