에드몬드-카프 알고리즘 (Edmonds-Karp Algorithm)
- 포드- 풀커슨 방법을 BFS로 구현한 알고리즘
2023.05.22 - [알고리즘] - 네트워크 플로우(Network Flow) 알고리즘, 포드-풀커슨 (Ford-Fulkerson)
네트워크 플로우(Network Flow) 알고리즘, 포드-풀커슨 (Ford-Fulkerson)
네트워크 플로우(Network Flow) 알고리즘이란? - 그래프에서 두 정점 사이에 얼마나 많은 유량(flow)을 보낼 수 있는지 계산하는 알고리즘 - 그래프 내 source 정점에서 유량을 발생시켜 간선을 통해 sink
sum-mit45.tistory.com
그렇다면, BFS를 사용하는 이유는 무엇일까??
1. 시간복잡도
E: 간선 개수, V: 정점 개수, F: 최대 유량이라고 했을 때,
DFS를 사용할 경우 시간복잡도는,
O((|E|*|V|)*F) 로 stack overflow(스택 오버플로우)가 발생할 가능성이 있다.
BFS를 사용한다면,
O(|V| * (|E|^2)의 시간복잡도를 가진다.
2. 가장 짧은 경로의 증가 경로 탐색
: 최단거리로 최대의 유량을 보냄 -> 중간에 용량이 1인 간선이 끼어 있어도, 돌아가는 길이면 무시
(1) 포드-풀커슨 (Ford-Fulkerson), DFS로 탐색하는 경우
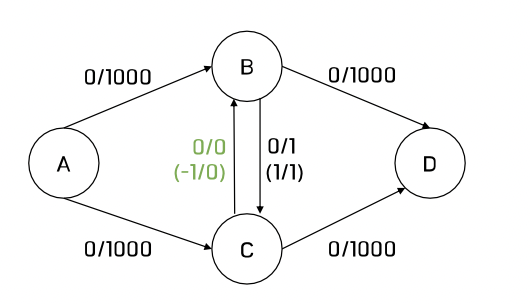
(1) A -> B -> C -> D: 1의 유량을 보냄
(2) A -> C -> B -> D: 1의 유량을 보냄(역간선)
(3) A -> B -> C -> D: 1의 유량을 보냄
(4) A -> C -> B -> D: 1의 유량을 보냄(역간선)
위 과정을 반복하고, ... ,
2000번의 탐색으로 최대 유량을 발견한다.
(2) 에드몬드-카프 (Edmonds-Karp Algorithm), BFS로 탐색하는 경우
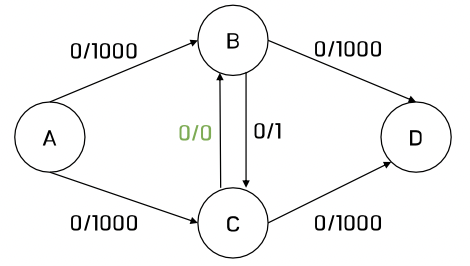
(1) A -> B -> D: 1000의 유량을 보냄
(2) A -> C -> D: 1000의 유량을 보냄
2번의 탐색으로 최대 유량을 발견한다.
에드몬드 - 카프 알고리즘 진행과정을 다시 한번 정리해보자면,
에드몬드 - 카프 (Edmonds-Karp) 진행과정
1. 네트워크에 존재하는 모든 간선(역방향 포함)의 유량을 0으로 초기화
2. source 에서 sink 로 갈 수 있는 잔여 용량이 남은 경로를 BFS 탐색
3. 해당 경로에 존재하는 간선들의 잔여 용량 중 가장 작은 값을 유량으로 흘려보냄
4. 해당 유량에 음수 값을 취해, 역방향 간선에도 흘려보냄 (-> 유량 상쇄를 위함)
5. 더 이상 잔여 용량이 남은 경로가 존재하지 않을 때까지 반복
C++ 코드
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#define MAX 10e9
#define INF 10e9
using namespace std;
vector <int> v[MAX];
int cap[MAX][MAX] = {0,}; //용량 - 0으로 초기화
int flow[MAX][MAX] = {0, }; //현재 유량 - 0으로 초기화
int pre[MAX] = {0, }; //현재 탐색 중인 증가 경로에서 이전 정점을 저장하여 경로를 기억하는 역할
int total_flow = 0; //최대 유량
void maxFlow(int source, int sink){
memset(flow, 0, sizeof(flow));
while(1){
queue<int> q;
memset(pre, -1, sizeof(pre));
q.push(source);
pre[source] = source;
while(!q.empty()){
int now = q.front();
q.pop();
if(now == sink) break;
for(int i=0; i<v[now].size(); i++){
int next = v[now][i];
//방문하지 않은 정점 중 용량이 남는 경우
if(cap[now][next] - flow[now][next] >0 && pre[next] == -1){
q.push(next);
pre[next] = now;
}
}
}
//더 이상 증가 경로 없음
if(pre[sink]==-1) break;
//증가 경로로 새로 흘러줄 유량 = 경로 중 최소 잔여 용량
int min_flow = INF;
for(int i=sink; i!=source; i=pre[i]){
int j = pre[i];
min_flow = min(cap[j][i] - flow[j][i], min_flow);
}
//증가 경로는 유량 증가, 역방향 경로는 유량 감소
for(int i=sink; i!=source; i=pre[i]){
int j=pre[i];
flow[j][i] += min_flow;
flow[i][j] -= min_flow;
}
total_flow += min_flow;
}
return;
}'알고리즘' 카테고리의 다른 글
| 네트워크 플로우(Network Flow) 알고리즘, 포드-풀커슨 (Ford-Fulkerson) (0) | 2023.05.22 |
|---|---|
| Hash (해시) (0) | 2022.03.14 |
| Binary Search (이진 탐색) (0) | 2022.03.13 |
