출처: 이기용 교수님, 데이터마이닝및분석 수업
7장에서는 클러스터링이 무엇인지와 대표적인 클러스터링인 (1) K-means, (2) Agglomerative Hierarchical Clustering, (3) DBScan에 대해서 배웠다.
이번에 정리한 내용은 DBSCAN에 대한 내용이다.
순서대로 전반적으로 정리하자면, 큰 주제는 DBSCAN이기에 첫 부분은 DBSCAN에 대한 전반적인 설명이다.
- Defining Density: '밀도'를 정의하기 위해 여러 방법이 있는데 여기서는 center-based approach 에 대해 설명한다. 핵심은 Eps 안에 있는 점의 수를 세어 측정하는 것이다.
- Classification of Points: DBScan에서 모든 점은 Core Points, Border Points, Noise Points 중 하나로 나뉘어진다.
- The DBSCAN Algorithm
- Selection of DBScan Parameters: 사용자 파라미터인 eps와 minpts를 어떻게 설정할 것인지에 대한 내용이다. 모든 data points 에서 k-dist를 계산한 다음, 급격한 보이는 거리를 eps로 그 때의 k값을 minPts로 사용한다.
- Clusters of Varying Density: 클러스터의 밀도가 크게 다른 경우에 DBScan에 문제가 발생할 수 있다.
- Strengths and Weaknesses: 장점은 nosie에 대한 저항성이 낮고, arbitary한 모양과 크기의 클러스터를 처리할 수 있고, k-means를 사용할 때는 찾을 수 없는 더 많은 클러스터를 찾을 수 있다는 것이다. 단점은 밀도가 크게 다를 경우 문제가 되고, 고차원으로 갈수록 의미가 없다, 계산 비용이 많이 든다는 것이다.
이런 순서대로 전개된다.
DBSCAN
: simple 하고 effective density-based 클러스터링 알고리즘
: low density 별로 서로 분리된 regions of high density → 고밀도 영역 = 클러스터
DBScan에서 알아야 할 내용들이다. 뒤에도 나오겠지만, 모든 점들을 이 세 점 중 하나로 포함시킨다.
- core point(핵심점): 주변 밀도가 높은 점
- border point(경계점): 밀도가 높지는 않지만, 가까운 점 중에 주변 밀도가 높은 점이 있으면 된다. cluster의 boundary에 해당하는 점.
- outlier: 주변 밀도가 낮고, 가까운 점 주변에 주변 밀도가 높은 점도 없다 → cluster에 껴주지 않고 알아서 버린다
Defining Density
: 밀도를 정의하기 위한 몇 가지 접근법이 있다.
: DBSCAN의 기반이 되는 center-based approach 에 대해 설명한다
Center-based approach
- density는 데이터 세트의 특정 지점에 대해 해당 지점의 specified radius(Eps, 지정된 반경) 내에 있는 점의 수를 세어 측정한다.
→ the point itself도 포함(그 점 자체도 포함한다) - 이 방법은 구현이 간단하지만 문제가 있다: 모든 점의 밀도는 specified radius(지정된 반지름) 에 따라 달라진다
따라서 반지름을 어떻게 정해야 하는가가 이슈이다.
- 반지름이 너무 크면(Eps가 너무 크면) → 모든 점이 다 주변에 점이 많다고 카운트 → 모든 점의 밀도가 비슷하다
- 반지름이 너무 작으면(Eps가 너무 작으면) → 모든 포인트의 density가 1이 된다.
Classification of Points
: DBSCAN에서 각 점은 세 가지 점 중 하나로 분류된다.
: MinPts 와 Eps 는 user-specified parameters 이다.
- Core Points: eps 안에 minpts 이상의 점이 나오면 core points
- 중심점은 밀집된 영역(클러스터)의 내부에 있는 점이다.
- 최소 MinPts 가 Eps 거리 내에 있는 경우 점은 core points 이다.
- Border Points(경계점): core point는 아니지만, eps 안에 core point가 존재할 때
- 경계점은 중심점이 아니지만 중심점의 거리 Eps 내에 있다(즉, 밀도가 높은 영역의 가장자리에 있음)
- 경계점은 여러 core points의 주변에 있을 수 있다
(어떤 border points는 서로 다른 cluster의 core points를 가질 수 있다 → 아무데나 보내줘도 상관X)
- Noise Points: 주변 밀도가 낮은 점. eps 안에 core points도, border points도 없는 경우
- 노이즈 포인트는 core points 나 border points 가 아닌 모든 포인트입니다( 즉, 점유율이 희박한 지역에 있음)
The DBSCAN Algorithm
[ Basic Idea ]
- (1개의 거리 eps 내에서) 충분히 가까운 two core points가 같은 클러스터에 배치된다.
→ core points로 묶인 애들을 모아서 cluster로 리턴 - 중심점에 충분히 가까운 경계점은 중심점과 동일한 클러스터에 배치된다.
- noise points는 버려진다. → outlier에 대한 고민X
[ Algorithm ]
- 모든 점을 core, border, noise points로 레이블 지정
- noise points 제거
- 서로 Eps 거리 내에 있는 모든 core points 사이에 edge를 배치 → 근거리의 점 연결
- 연결된 core points를 각 그룹으로 별도의 cluster로 만들기 → 모인 점을 cluster 로 리턴
- 각 border points 을 연결된 core points의 클러스터 중 하나에 할당
Selection of DBSCAN Parameters
: parameters Eps와 MinPts를 어떻게 설정할 것인지
[ Observation ]
k-dist: 점에서 k번째 가장 가까운 이웃까지의 거리
1-dist: 나랑 가장 가까운 점과의 거리
- 일부 cluster에 속하는 points의 경우 → k가 cluster size보다 크지 않다면 k-dist가 작다
- cluster에 있지 않은 points의 경우 → k-dist가 상대적으로 크다 (ex. noise points)
- cluster 안에 있는 값이라면 k값이 커짐에 따라 거리가 급격하게 증가하지 않지만, outlier의 경우에는 k값에 따라 거리가 급격하게 커질 수 있다.
[ Basic approach ]
- 모든 data points에서 k-dist를 계산
- 오름차순으로 정렬한 다음 정렬된 값을 표시
- k-dist 값에서 급격한 변화가 보이면 → 이 거리를 Eps로 간주하고, 그 때의 k값을 MinPts로 사용한다
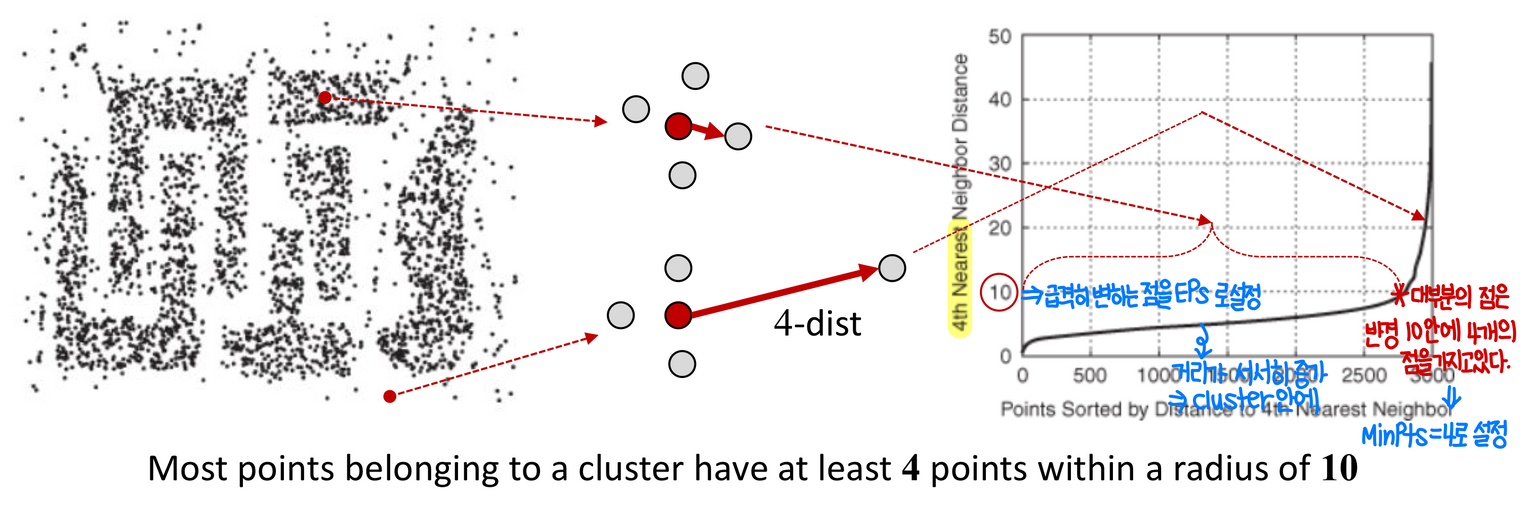
[ Results ]
- k-dist < Eps → core points
- k-dist > Eps → noise points/border points
이 방법으로 결정된 Eps 값은 k에 따라 달라진다. → 그러나 k의 변화에 Eps가 급격하게 바뀌는 것X
- k가 너무 작으면 → noise이나 outlier도 cluster로 레이블이 지정될 수 있다
- k가 너무 크면 → small clusters은 noise로 지정될 가능성이 높다
원래 DBSCAN 알고리즘은 대부분의 2차원 데이터 세트에 적합한 값으로 k = 4의 값을 사용한다
Clusters of Varying Density
: 클러스터의 밀도가 크게 다를 경우 DBSCAN에 문제가 발생할 수 있다.
: 예시) Eps 값이 고정된 경우
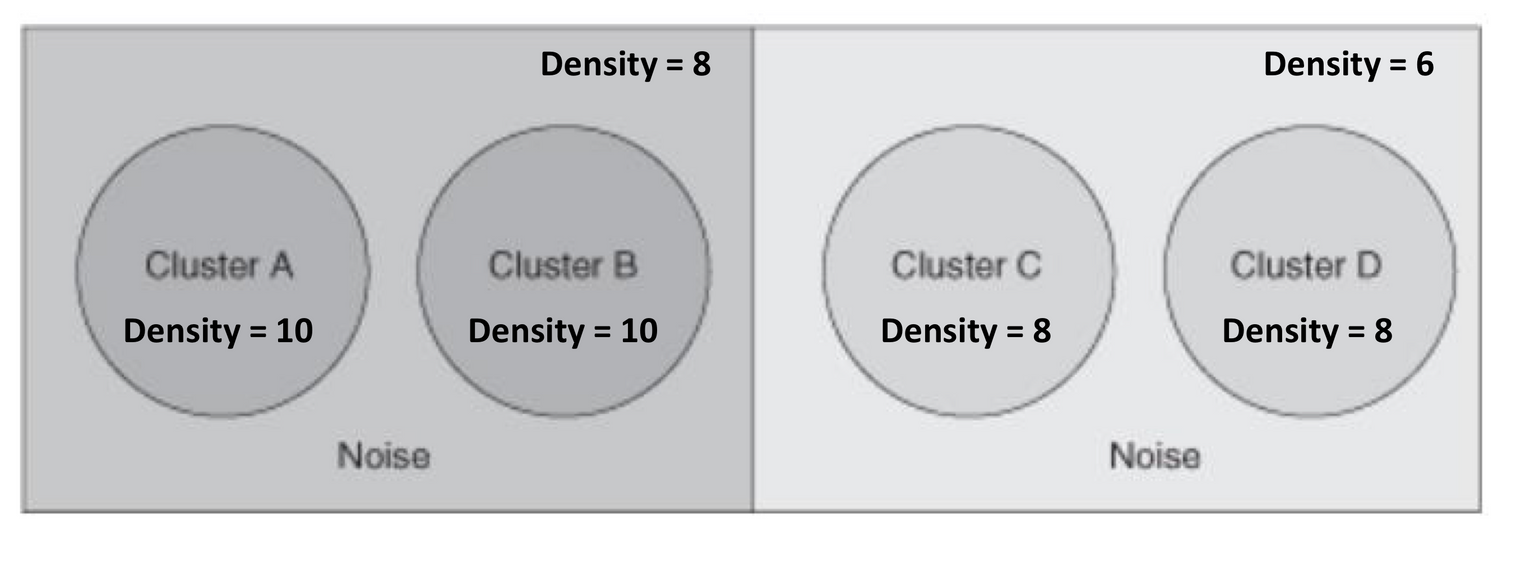
- 사람이 보기에는 Cluster A, B, C, D를 구분할 수 있다.
- MinPts=7 라고 한 경우 → Cluster C와 D는 그 주변과 구분하여 Core Points로 구분되지만, 왼쪽은 Clusters를 하나로 인식하여 왼쪽을 larger cluster 로 파악한다 (더 진한 밀도를 찾지 못함)
- MinPts=9 라고 한 경우 → Cluster A와 B는 Core Points로 구분되지만, 오른쪽은 Clusters를 구분하지 못하고 하나의 noise 가 되는 문제가 발생.
: k-means는 복잡한 그림을 절대 찾을 수 없지만, DBSCAN은 훨씬 잘 찾는다. 다만 Eps와 MinPts를 찾는 게 어렵다.
Strengths and Weaknesses
[ Strenghts ]
- 클러스터의 density-based 정의를 사용하기 때문에 noise에 대한 relatively resistant(상대적 저항성) → partial cluster
- 밀도를 기반으로 클러스터가 구성되므로, arbitrary shapes and size(임의의 모양과 크기)의 클러스터를 처리할 수 있다
- K-means을 사용하여 찾을 수 없는 많은 clusters을 찾을 수 있다
[ Weaknesses ]
- 클러스터의 densities가 크게 다를(widely) 경우 문제 발생
→ 지역에 따라 상대적인 밀도가 변할 때 이 값을 control 할 수 없음 - high-dimensional data에 대해 문제 발생: 고차원으로 갈수록 밀도의 개념이 많이 망가진다.
→ 밀도는 이러한 데이터에 대해 정의하기가 더 어렵기 때문.
→ 고차원으로 가면 공간이 폭발적으로 늘어나기 때문에 점 사이의 거리가 모두 멀어져서 다 비슷비슷 해짐. - 가장 가까운 이웃의 계산이 all pairwise proximities를 계산해야 하는 경우 비용이 많이 들 수 있습니다
각 점에 대해서 core/border/noise 를 판단하기 위해 모든 점을 확인해야 하는데 특별한 기술이 없으면 찾기 힘들다.


